A non-Iterative way for preliminary designing Plate & Frame Exchanger

Originally posted on

Tools for design #

In the well-known chemical engineering text book Plant Design and Economics for Chemical Engineers, Timmerhaus has provided a non-iterative NTU method to calculate P&F HXchanger plate count & heat coefficients; given some geometry info about plates. This method differs from the iterative method given by R.K Sinott in his book, Coulson & Richardson’s Chemical Engineering, Vol.6.

Iterative solutions can be scripted with relative ease but for process engineers in field sequential calculations are more doable with a handheld calculator. It must however be stated that Timmerhaus method does require some non-linear solver for converging a relatively complex equation. Such solvers are available in programmable calculator like HP Prime & Ti 84. Also Android applications like Mathway & Smath Studio will do the trick, the latter is used here. In addition to that we will reproduce the problem in a free P&F simulation & rating application PHE Works.

It must be acknowledged that both solutions by Timmerhaus & Sinott are preliminary in nature & doesn’t consider influencing factors like corrugation geometry, pitch & chevron \(\beta\) angle however both books does include \(\beta\) angle (\(30^\circ\)) effects on pressure drop. \(\Delta P\) calculations are similar for both methods & willn’t be discussed here.

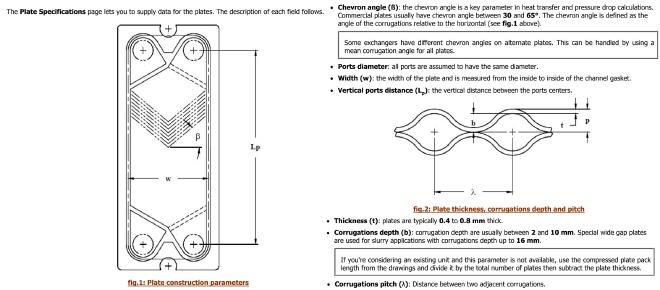
Care must be exercised when inputting mechanical specifications in PHE Works. Timmerhaus & Sinott while phrasing plate distance/spacing clearly means the flow region available to the fluid. There is no input box for Plate Spacing in PHE Works as a workaround we will study above picture taken from its help manual. It can be seen that

$$ \text{Plate Spacing} = \text{Corrugation Depth} - \text{Plate Thickness} $$

so in order to have a spacing of \(3 \ \text{mm}\) (as given in Coulson’s example) in the input box of corrugation depth (parameter \(b\)) we will add thickness (\(0.75 \ \text{mm}\)) such that the final value of \(b\) is \(3.75 \ \text{mm}\).

Timmheraus NTU method #

PHE Works results #

Conclusion #

1. Striking resemblance in overall heat transfer coefficients (service); \(2059 \text{ W}/(^\circ\text{C}\cdot\text{m}^2)\) via Timmerhaus method & \(2189 \text{ W}/(^\circ\text{C}\cdot\text{m}^2)\) via PHE Works
2. Some deviations can be attributed to fluid/metal physical properties databank & factors that PHE Works does take into account like \(\beta\), corrugation pitch. This can be seen in slightly low number of plate count application predicted; 86 versus 91
3. Port velocities are very high at water side so that needs a rectification

All files & Coulson example pdf are uploaded here. For Timmerhaus method consult Example 14.7 in the 5th edition of his book.